二、2020年广东省高等高等学校
招收中等职业学校毕业生统一考试
数学科考试说明
(一)考试性质
广东省高等职业院校招收中等职业学校毕业生考试是以职业高中、中等专业学校和技工学校应届毕业生为对象的选拔性考试。有关普通高等学校将根据考生成绩,按已确定的招生计划,德、智、体全面衡量,择优录取。因此,本考试应具有较高的信度、效度以及必要的区分度和适当的难度。
(二)考试内容
数学科考试旨在测试考生对数学的基础知识、基本技能和基本的数学思想方法的掌握程度,以及观察能力、空间想象能力、分析与解决问题能力和数学思维能力。考试内容的确定主要根据教育部颁布的《中等职业学校数学教学大纲》,并结合了广东省中等职业技术教育的实际。对知识的认知要求分为了解、理解和掌握三个层次。
各项考试内容和要求如下:
1.集合与逻辑用语
考试内容:
(1) 集合及其运算。
(2) 数理逻辑用语。
考试要求:
(1)理解集合、元素及其关系,理解空集的概念。
(2)掌握集合的表示法及子集、真子集、相等之间的关系。
(3)理解交集、并集和补集等运算。
(4)了解充要条件的含义。
2. 不等式
考试内容:
(1)不等式的性质与证明。
(2)不等式的解法。
(3)不等式的应用。
考试要求:
(1)理解不等式的性质,会证明简单的不等式。
(2)理解不等式解集的概念。掌握一元一次不等式、一元二次不等式的求解。
(3)了解含有绝对值的不等式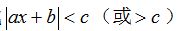 的求解。 的求解。
(4)会解简单的不等式应用题。
3. 函数
考试内容:
(1)函数的概念。
(2)函数的单调性与奇偶性。
(3)一元二次函数。
考试要求:
(1)理解函数的概念、定义及记号,了解函数的三种表示法和分段函数。
(2)理解函数的单调性和奇偶性,能判断一些简单函数的奇偶性和单调性。
(3)掌握二次函数的图像和性质及其简单应用。
4.指数函数与对数函数
考试内容:
(1)指数与指数函数。
(2)对数及其运算,换底公式,对数函数,反函数。
考试要求:
(1)了解n次根式的意义。理解有理指数幂的概念及运算性质。
(2)理解指数函数的概念。理解指数函数的图像和性质。
(3)理解对数的概念(含常用对数、自然对数)及运算性质,能进行基本的对数运算。
(4)理解对数函数的概念。了解对数函数的图像和性质。
(5)通过指数函数与对数函数的关系,了解反函数的概念及互为反函数的函数图像间的关系;会求一些简单函数的反函数。
5.三角函数
考试内容:
(1)角的概念的推广及其度量,弧度制。任意角的三角函数。单位圆中的三角函数线。
(2)同角三角函数的基本关系式。正弦、余弦的诱导公式。
(3)和角公式与倍角公式。
(4)正弦函数、余弦函数的图像和性质。
(5)余弦定理、正弦定理及其应用。
考试要求:
(1)理解正角、负角、零角的概念。理解弧度的意义,能进行角度与弧度的换算。
(2)理解任意角的正弦、余弦、正切的定义。
(3)掌握三角函数值的符号;掌握特殊角的正弦、余弦、正切的值;理解同角三角函数的基本关系式: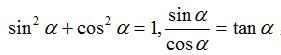 和正弦、余弦的诱导公式。能由已知三角函数值求指定区间内的角的大小。 和正弦、余弦的诱导公式。能由已知三角函数值求指定区间内的角的大小。
(4)理解两角和的正弦、余弦公式;了解两角和的正切公式;了解两倍角的正弦、余弦、正切公式。
(5)能正确运用三角公式进行简单三角函数式的化简、求值。
(6)掌握正弦函数的图像和性质。了解函数的周期性和最小正周期的意义。了解余弦函数的图像和性质。
(7)理解正弦定理和余弦定理,会解斜三角形的简单应用题。
6.数列
考试内容:
(1)数列的概念。
(2)等差数列。
(3)等比数列。
考试要求:
(1)了解数列的概念。理解等差数列和等比数列的定义。
(2)理解等差中项公式、等差数列的通项公式与前n项和的公式。
(3)理解等比中项公式、等比数列的通项公式与前n项和的公式。
(4)会解简单的数列应用题。
7.平面向量
考试内容:
(1)向量的概念,向量的运算。
(2)轴上向量的坐标及其运算;平面向量的直角坐标运算。
(3)两个向量平行(共线)的条件;两个向量垂直的条件。
(4)中点的平移公式;中点坐标公式;两点间距离公式。
考试要求:
(1)了解向量的概念、向量的长度(模)和单位向量。理解相等向量、负向量、平行(共线)向量的意义。
(2)理解向量的加法与减法运算及其运算法则。
(3)理解数乘向量的运算及其运算法则。理解两个向量平行(共线)的条件。
(4)理解向量的数量积(内积)及其运算法则。理解两个向量垂直的条件。
(5)了解平面向量的坐标的概念,理解平面向量的坐标运算。
(6)掌握中点坐标公式和两点间距离公式。
8.平面解析几何
考试内容:
(1)曲线方程。曲线的交点。
(2)直线方程。
(3)圆的标准方程和一般方程;圆的参数方程。
(4)椭圆、双曲线和抛物线的标准方程及其几何性质。
考试要求:
(1)理解曲线与方程的对应关系。掌握求曲线交点的方法。
(2)理解直线的斜式方程、斜截式方程、截距式方程、一般式方程,能根据条件求出直线方程。
(3)理解两条直线的交点的求法;理解两条直线平行与垂直的条件;了解点到直线的距离公式。
(4)掌握圆的标准方程和一般方程;了解圆的参数方程。
(5)能根据给定直线、圆的方程判断直线与圆的位置关系;能根据给定两个圆的方程判断两圆的位置关系。
(6)理解椭圆的标准方程和性质,了解双曲线和抛物线的标准方程和性质。
9.概率与统计初步
考试内容:
(1)分数、分步计数原理。
(2)随机事件和概率。
(3)概率的简单性质。
(4)直方图与频率分布。
(5)总体与样本。
(6)抽样方法。
(7)总体均值、标准差;用样本均值、标准差估计总体均值、标准差。
考试要求:
(1)理解分数、分步计数原理。
(2)理解随机事件和概率。
(3)理解概率的简单性质。
(4)了解直方图与频率分步。
(5)了解总体与样本。
(6)了解抽样方法。
(7)了解总体均值、标准差及用样本均值、标准差估计总体均值、标准差。
(三)考试形式及试卷结构
考试采用闭卷笔试形式,全卷满分150分,考试时间为120分钟。
试题分为选择题、填空题和解答题三种题型,其中:选择题15题,每题5分,共75分;填空题5题,每题5分,共25分;解答题4题,共50分。选择题是“四选一”型的单项选项题;填空题只要求直接写出结果,不必写出计算或推演过程;解答题包括计算题、证明题和应用题等,解答题应写出文字说明、演算步骤或推证过程。
试题按其难度(平均得分率)分为容易题、中等题和难题,平均得分率在0.7以上者为容易题、在0.3~0.7之间为中等题、在0.3以下者为难题,三种试题分值之比约为2:2:1.
(四)题型示例
|